BUAA_2025_Unit1_表达式解析与递归下降

架构设计迭代

第一次作业分析

1.1UML类图

UML

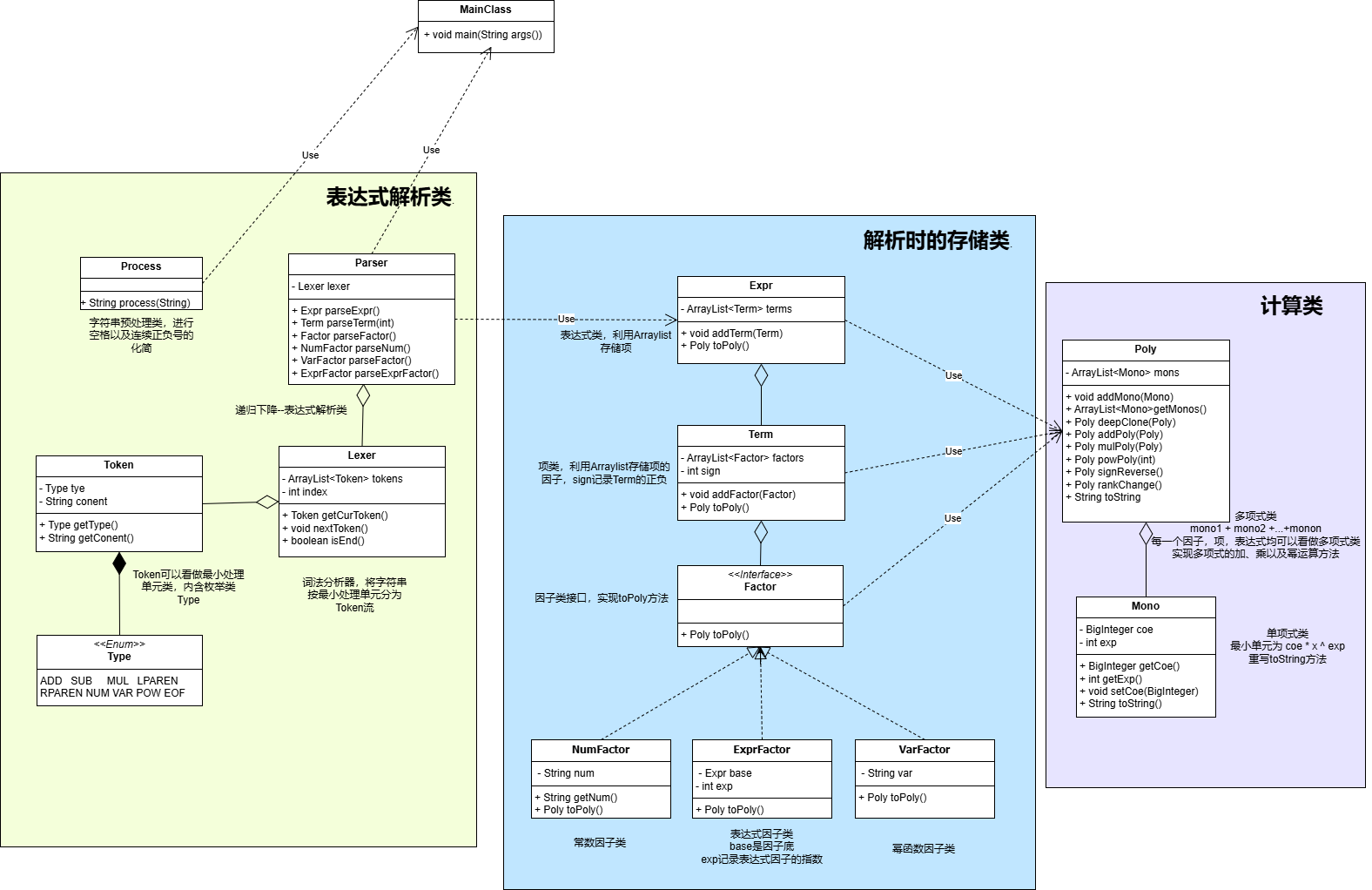
1.2架构分析

进过对指导书的分析，我们不难将整个任务分为三部分

  • 表达式的解析：负责将输入字符串进行处理，按最小逻辑处理单元分为有序的Token流，之后依据形式化表述进行Expr,Term,Factor的递归下降解析
  • 表达式解析后的存储：依据指导书，将解析后的表达式利用容器存储为Expr,Term,Factor,且各级存储均实现计算类的toPoly()方法
  • 计算类：此次作业要求展开括号，实际上都是多项式间的运算。我们可以将各级存储单元转为Poly,之后利用Poly的加法、乘法、幂运算进行计算
表达式的解析
输入预处理

在Process类中进行输入字符串的初步化简，主要包含以下几个方面

  • 去除空白项
  • 将连续正负号变为一个符号
  • 将^+021类似的^后面可能得正号去除掉
递归下降解析
  • Token：在Token类中包含了枚举类型Type,主要用于在Lexer中遍历输入时进行划分为最小处理单元并按照Token进行存储,例如
  • Lexer:遍历输入字符串，将输入划分为Token流，如+、-、012<num>等
  • Parser: 通过ParserExpr()、ParserTerm()、与ParserFactor()层层深入解析输入，分别返回Expr,Term,Factor,而幂函数因子、常数因子与表达式因子分别实现Factor接口

在解析Term的时候，我为Term设置了sign来记录这一项的正负。但是我在第三次迭代时Term的求导方法实现中遗漏了符号处理。其实可以在解析存储时就可以将项的-号作为一个-1的因子添加到factors中

基本计算单元处理

分析形式化表述，我们可以得到所有存储层次都可以化为多项式的形式，而多项式又是单项式构成的

单项式Mono与多项式Poly的设计形式如下，其中Poly中利用容器存储了Mono
$$
mono = ax^b
$$

$$
poly = \sum_{i=1}^{n} a_{i}x^{b_{i}}
$$

为Expr,Term,Factor等实现toPoly()方法，调用expr.toPoly()方法可以将整个输入转换为一个多项式

  • Factor的toPoly():常数因子转换为只含有一个单项式的指数为0的多项式，幂函数转换为只含有一个单项式的系数为1的多项式。表达式因子的toPoly() 中先调用base的toPoly()方法得到一个多项式，再调用Poly的powPoly(exp)方法得到表达式因子的多项式

    1
    return base.toPoly().powPoly(this.exp);

  • Term的toPoly()：遍历所有factor，调用各因子的toPoly后使用mulPoly乘起来

    1
    2
    3
    4
    for (Factor factor : factors) {
      poly = poly.mulPoly(factor.toPoly());    
    }
    return poly;

    此外，有一个细节需要注意，对poly可以先初始化成一个为1的多项式以及项的符号的处理

  • Expr的toPoly():将其含有的所有的项的Poly形式调用addPoly加起来

    1
    2
    3
    4
    for (Term term : terms) {
      poly = poly.addPoly(factor.toPoly());    
    }
    return poly;
计算单元分析

  • Mono:coe存储单项式的系数，exp存储单项式的指数，并且重写toString()方法，实现单项式的coe*x^exp形式的输出，输出优化可见后面优化部分

  • Poly:使用容器存储mono,同样需要重写toString方法，使用+号将各mono的输出连接起来

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    // 1.addPoly
    Poly poly = deepClone(this);
    for(Mono mono1 : other.getMonos()) {
        for(Mono mono2 : poly.getMonos() ) {
            int flag = 1;
            if(mono2.getExp() == mono1.getExp()) {    // 此处可以在Mono中重equals方法，实现个性化比较，同时避免直接对外暴露指数
                mono2.setCoe(mono2.getCoe().add(mono1.getCoe()));
                flag = 0;
                break;
            }
            if(flag == 0) {
                poly.addMono(mono1);
            }
        }
    }

    我在Poly的各个计算方法中，在运算前首先深克隆自身，再对克隆出来的对象做修改，不直接改变源对象本身

    Poly的乘法依旧使用两层循环完成，幂运算调用乘法完成

    注意同类项的合并

1.3Bug分析

比较幸运的是，我自己在此次强测和互测中并没有出现bug

在第一次作业房间中，我利用评测机刀中了我们房间唯一一次，有一位同学的项目在输入字符串的最后如果有空白字符会报错。他是没有做预处理操作，而是在解析时会讨论该处有无空格，但似乎漏了字符串最后的空白字符。个人认为这样处理比较麻烦，且容易遗漏某处可能出现的空白字符。

1.4性能优化

Mono中优化

  • 系数为0的时候直接返回空

  • 指数为0，直接输出系数

  • 系数为-1时候只输出-号，系数为1时候不输出

  • 指数为1，不输出

    以上优先级依次递减

Poly中优化

如果Mono的toString为空则不做处理，不为空则用+号连接

如果有正的项，一定将正的项放在前面，可以少一个-号

如果最后答案为空，输出0

第二次作业分析

2.1 UML类图

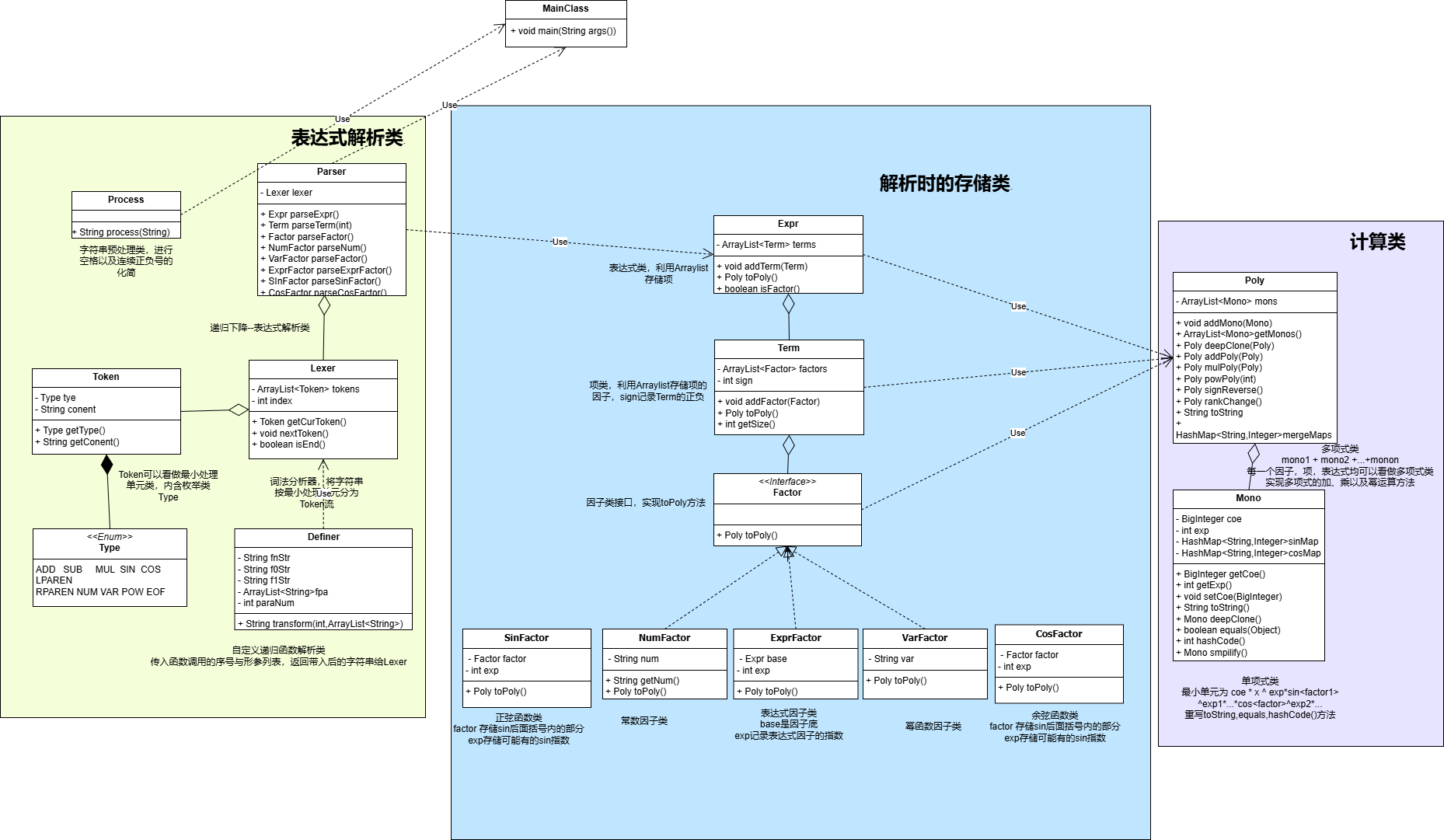
第二单元UML类图

2.2 三角函数与自定义递归函数迭代

分析指导书我们可以得到，此次的更新之处主要有新增三角函数因子，自定义递归函数

三角函数的解析与Mono最小处理单元的改变

新增三SinFactor与CosFactor类，类中有两个成员变量——factor(记录三角函数括号内的因子)与exp（记录三角函数的指数部分）

在Parser中新增parseCosFactor()和parseSinFactor()方法

由于三角函数的引入，我们的最小处理单元不可以再是 a*x^n形式了，而是变成了

$$ ax^n*\prod_{i=1}sin(factor_i)^{{exp}_i}*\prod_{j=1}cos(factor_j)^{{exp}_j} $$

在Mono中新增成员变量sinMap与cosMap

1
2
private HashMap<String, Integer> cosMap; //所有cos括号里的内容及其指数
private HashMap<String, Integer> sinMap; //所有sin括号里的内容及其指数

HashMap中的String字符串是sinFactor中的factor.toPoly().toString()方法得到的

由于后续sin^2+cos^2=1和二倍角的优化与sin括号中的内容(HashMap的键)息息相关，需要保证mono完全相同的多项式调用toString()输出的结果相同，我在Poly中设计了一个rankChange()方法调整monos的顺序，保证等价的多项式输出顺序一定。通过toPoly().rankChange().toString()方法输出字符串。

在Poly类中调整addPoly()、mulPoly()、powPoly()方法细节。为了计算过程中识别同类项方便，我在Mono中重写了equals()与hashCode()方法，在两个mono的幂指数，sin与cos完全相同时返回真。

自定义递归函数解析

为了实现自定义函数的解析，我们设置了Definer工具类，用于实现自定义函数递归调用的解析

成员变量fnStr,f0Str,f1Str分别记录递归函数的定义列表的=右边的部分

fpa记录形参列表，paraNum记录参数个数

我们在Lexer中遍历解析时候，如果碰到字符f，则认为遇到了递归函数调用因子，我们依据形式化表述定义

$$ f\{序号\}(factor1[,factor2]) $$

解析出其中调用因子的序号n,以及参数列表，传递给Definer类中的transform方法，得到函数因子带入函数表达式后的结果字符串，在Lexer中用该结果字符串替换待解析表达式的函数调用因子，之后从原处继续遍历解析

transform方法基本如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public String transform(int n, ArrayList<String>args){
    if(n==0 || n==1){
        // 用实参列表args替换f0Str或者f1Str得到结果返回
        replace str
        return
    }
    else {
        ans = replace fnStr   // 先将实参代入fnStr中
        ...
        str1 = transform(n-1,args1)    // 找出n-1的实参并进行递归调用
        str2 = transform(n-2,args2)
        ans = repalce str1&str2
        return
    }
}

在自定义函数替换与解析时候，有以下几点需要注意

  • 在将实参代入函数初始表达式时候，一定要给实参套上()
  • 将transform结果替换至表达式原函数调用因子处时，也要套上()
  • 识别实参时，,一定识别准确，确保其不属于外层函数调用的某一个实参因子
  • 如果是两个参数的自定义函数，替换实参时一定要设置好过渡字符。例如形参列表(y,x)，在将y换为第一个带x

的实参后，如果直接再将x换位第二个实参，会导致将第一个实参代入产生的x也替换为第二个实参。

2.3BUG分析

我在此次作业的强测和互测中均出现了bug,主要是由输出格式问题引起的format error

对于sin()及cos()输出时候,如果括号中的不是一个因子，需要再套一层括号。为此，我设计了一个isFactor方法，在表达式只有一个项并且这个项只有一个因子时候返回真。但是对于项中只有一个因子并且该项同时有一个符号时，例如sin(-x)错误的判断为了因子，没有加应有的括号。

还有一个由于二倍角优化的bug可以见下面优化处详解

在互测环节中，我针对上述自定义函数解析时候注意点构造了对应测试样例，例如f{2}(f{1}(x^2,x^4,x^3)等；还利用了测评机进行了自动化测试。

2.4输出优化

此次作业的优化主要是针对三角函数进行的，我进行了2sin(x)cos(x)=sin(2x)以及a*m*cos(x)^2+b*m*sin(x)^2 =(a-b)*m*cos(x)^2+bm 的化简

还有sin(0)与cos(0)的输出优化

二倍角化简

我在Mono中增加了simplify()方法进行二倍角化简，伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public Mono simplify() {
    if(sinMap == null || cosMap == null)
        return;
    for (String s : new ArrayList<>(sinMap.keySet())) {
        if(coe is not even number) return; // 系数不是偶数，直接返回
        if(sinMap.get(s) == 0) continue;
        if(cosMap.containsKey(s) && cosMap.get(s)!=0){
        int sinExp,cosExp,minExp; 
        if(coe含有因子2的最大个数大于minExp){ // 确保此次化简至少可以减少sin或者cos
            ...
            cnt次二倍角
            ...
            sinMap.put(sin(2x),cnt); 
        }
        }
    }
    return this
}
sin^2+cos^2化简

我是在Poly的addMono()方法中进行该部分的化简，在每次为多项式加上一个单项式均会检查是否可以进行相应化简，但是该方法也导致了我第三次作业中一个测试点TLE

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public void addMono(Mono other) {
    for (Mono mono: this.monos) {
        for(String s : mono.sinMap.keySet()){
            if(mono 除去sin(s)^2 并且 other除去cos(s)^2的equals()为真) {
                // 前提是mono与other还有相应因子，equals不比较系数
                // mono = a*m*sin(s)^2 && other = b*m*cos(s)^2
                //  a*m*sin(s)^2 +  b*m*cos(s)^2 = (a-b)*m*sin(s)^2+b*m
                mono.coe = a-b; other = b*m;
                monos.add(other);
                return;
            }
        }
        for{
            遍历cosMap
            if(...){... return}
        }
    }
    monos.add(other)
    return;
}
优化带来的bug

由于我在二倍角优化结束之后直接利用了HashMap.put()方法将产生的sin(2x)加入sinMap中，但这会导致sinMap原有的sin(2x)项被覆盖，导致错误。例如输入4*sin(2)*sin(1)*cos(1)会输出2*sin(2)。我之后做了如下修改：

1
2
3
sinMap.put(expr.toPoly().rankChange().toString(),
        !sinMap.containsKey(expr.toPoly().rankChange().toString()) ? cnt :
                sinMap.get(expr.toPoly().rankChange().toString()) + cnt);

虽然是第二次迭代产生的bug,但是它活过了第二次以及第三次作业的强测和第二次作业A房的狂轰乱炸，在第三次作业互测中不幸落败。非常感谢帮我发现这个bug的同学，我对hashMap的使用又谨慎了一点。

第三次作业分析

3.1UML类图

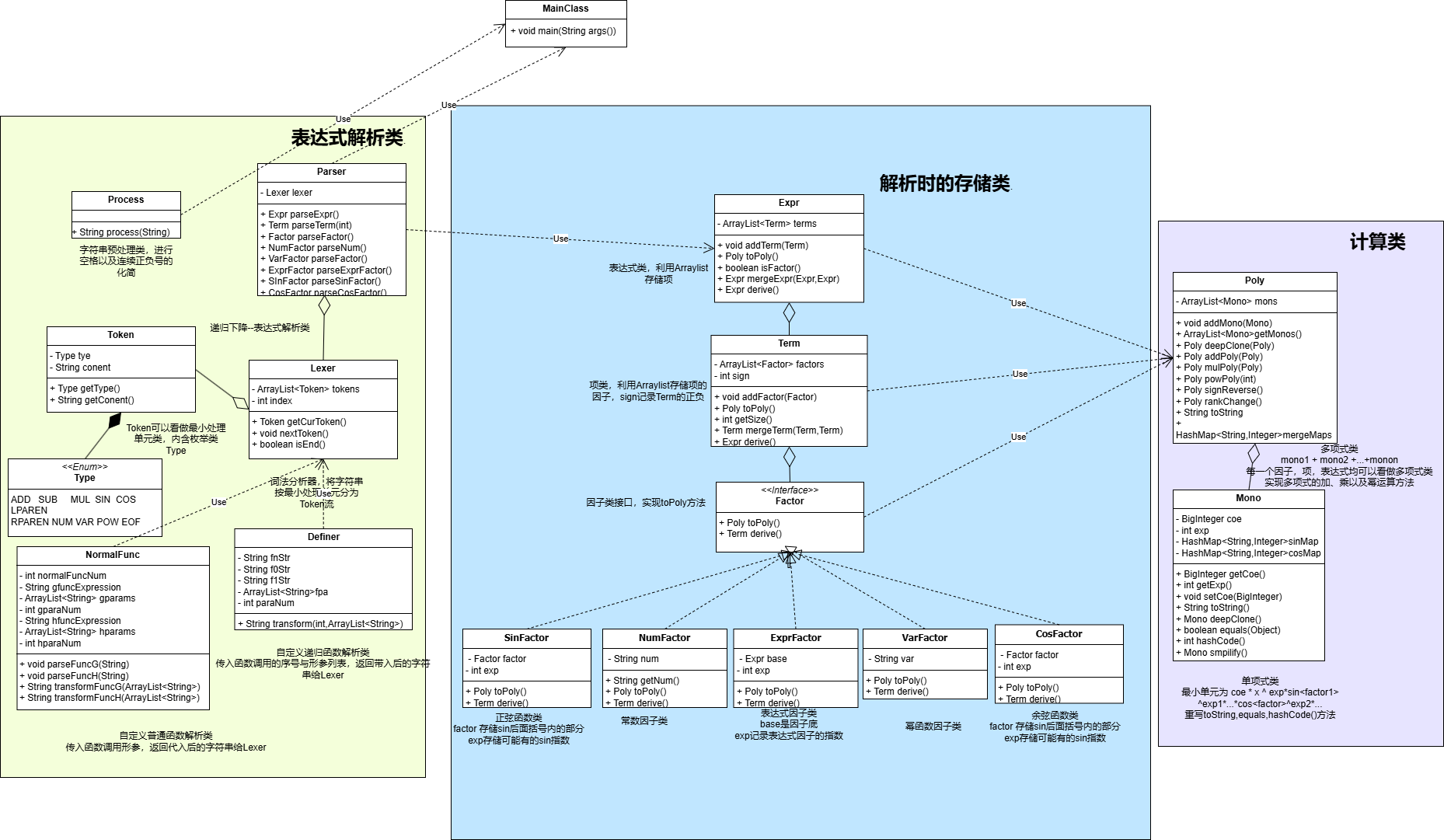
第三次作业

3.2自定义普通函数与表达式求导

自定义普通函数

与自定义普通函数类似，我新建了NormalFunc类，在其中存储了自定义函数的函数表达式以及形参列表，形参个数，实现transform()方法，在Lexer中遇到自定义函数后识别实参传给transform()并将传回的字符串替换至原有自定义普通函数因子调用处

求导的实现

  • Factor的求导：方法定义为public Term derive(),因子各自实现

  • Term的求导：伪代码如下(感觉也不伪了)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    public Expr derive(){
        Expr expr = new Expr();
        for(i=0; i<factors.size();i++){
            Term term = factors.get(i).derive();
            for(j=0;j<factors.size();j++){
                if(i!=j)
                    term.addFactor(factors.get(j))
            }
            expr.addTerm(term);
        }
        return expr;
    }

  • Expr的求导：遍历terms，将每个term求导的结果用mergeEexpr()合并起来

3.3BUG分析

很不幸，我又出现了bug(中测截止前没有好好测试，在互测中自己随便捏的第三个测试点就测出了自己的bug)

问题还是出在了Term的sign符号位上了：在对Term求导时不仅要对factors的因子求导，还有前面的符号位也要求导，导致了符号为负的项的求导全部是错的

互测中，我还是着重对sin(0)以及sin(3*x-x*3)等类似自己写作业时感觉容易出错的地方进行了针对性测试

3.4输出优化

与第二次作业基本相同

缺点分析

  • 接口实现 Term和Expr也实现了与因子相同的toPoly()方法与derive()方法，三个层次结构完全可以通过一个接口同一管理，而因子类再单独实现一个接口进行对因子类的统一管理(或者不实现，就用统一接口进行管理)
  • 封装不完善：在个别类的成员变量中，甚至同时实现了get()和set()方法，这还要private干什么 ,。为了安全性考虑，同时需要通过状态转化使得get方法得到的状态变量与存储的成员变量并不完全是同一种形式，也就是对外展现与内部存储形式不统一

新的迭代场景中的可扩展性

考虑学长博客 中提到了求和函数的解析，给出求和符号标志和求和上下界以及待求和因子的形式，我认为在当前作业架构中比较容易实现。

实现一个sumFuncFactor类，存有成员start,end,factorString和ansString分别代表上下界以及待求和字符串形式的因子和字符串形式的求和结果。在其中实现sum()方法和parse()方法，前者利用字符串替换和循环求出ansString，然后利用parse()解析为一个exprFactor对象并返回。在parser中新增parsesumFuncFactor()方法，利用识别到的参数构造出一个sumFuncFactor对象,调用其parse()方法得到一个因子，加入到项中，实现层次化解析。

BUG分析总结

由前面三次作业的bug分析可得，我的bug来源主要来自于以下两个方面

  • 对于Term的符号位的处理：hw2中对于符号为负的只含有一个因子的项的输出格式错误(是Mono中的isFactor()方法问题)，hw3中项的求导没有充分考虑符号位(Term中的derive()方法)。但是这个错误完全可以通过在解析时候为该项多添一个-1的因子来解决，方便简洁
  • 三角函数优化产生的问题：在Mono的simpify()方法中简单粗暴的HashMap.put()导致原有数据的覆盖。

总而言之，以上出现的bug完全可以通过更好的细节处理来实现

我在互测当中主要通过评测机以及针对自己认为的易错点进行针对性构造样例测试，并未根据被测程序结构来设计测试样例。

程序结构的度量

Statistic代码规模统计

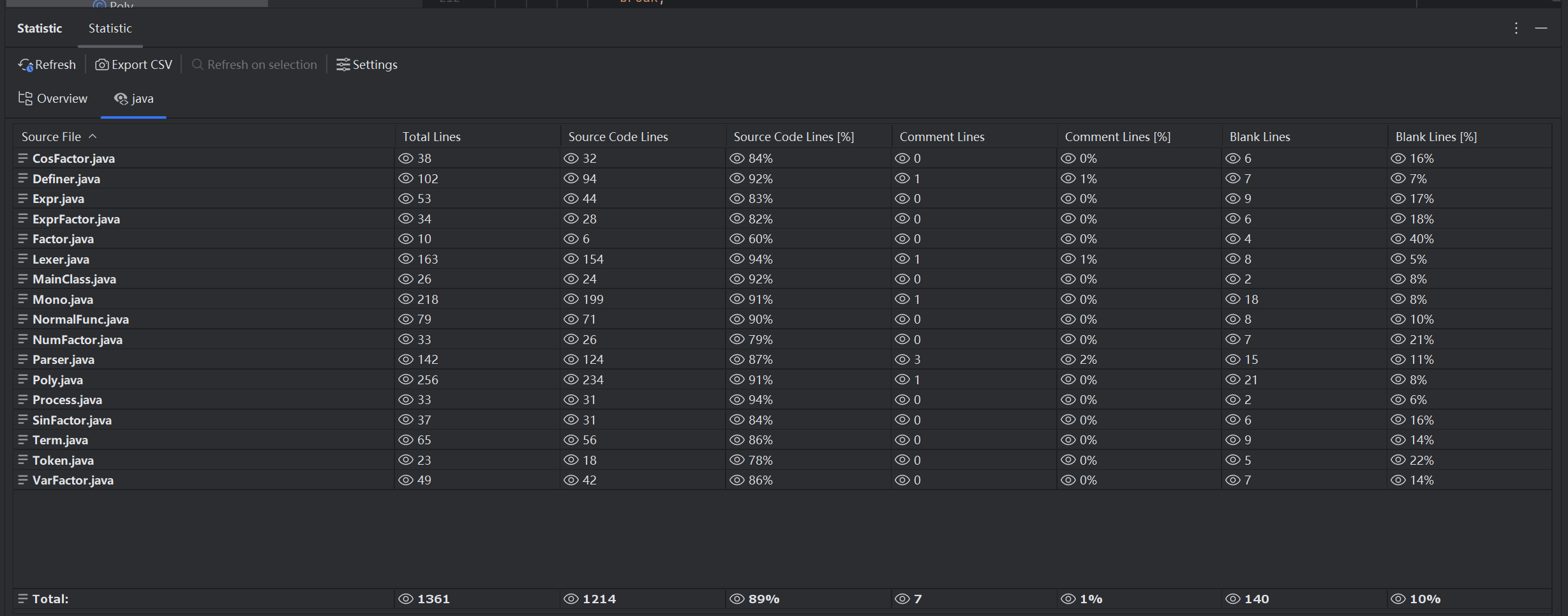
代码规模统计

如图可以看出，此次作业的代码行数达到了1361行，可能是我写字数的最多的作业了（OO作业是真养人啊）。从中可以看出Mono和Poly,Parser等计算类和解析类的代码行数比较多，这当然与其伟大的职责密不可分了。相反的，Factor以及Term等存储类的代码规模就比较小了。

从中可以看出Comment Lines占比比较小，可能注释的并不充分，希望在之后的OO作业中有所改善。

Method metrics复杂度分析

  • CogC认知复杂度:衡量理解代码所需的认知努力，通过计算代码中的嵌套结构和逻辑操作来评估复杂性
  • ev(G)基本复杂度：表示代码中不可化简的复杂度，衡量控制流路径的数量
  • iv(G)设计复杂度：评估代码的设计质量，衡量模块之间的依赖关系。
  • v(G)圈复杂度：衡量代码独立路径的复杂度，与跳转和分支结构相关。该复杂度越高，测试和维护越困难
  • OCavg平均操作复杂度：类中每个方法的平均圈复杂度
  • OCmax最大操作复杂度:类中单个方法的最高圈复杂度
  • WMC类的加权方法复杂度：类中所有方法的加权复杂度之和

由于项目中方法太多，截取其中复杂度过高的加以分析介绍

类复杂度

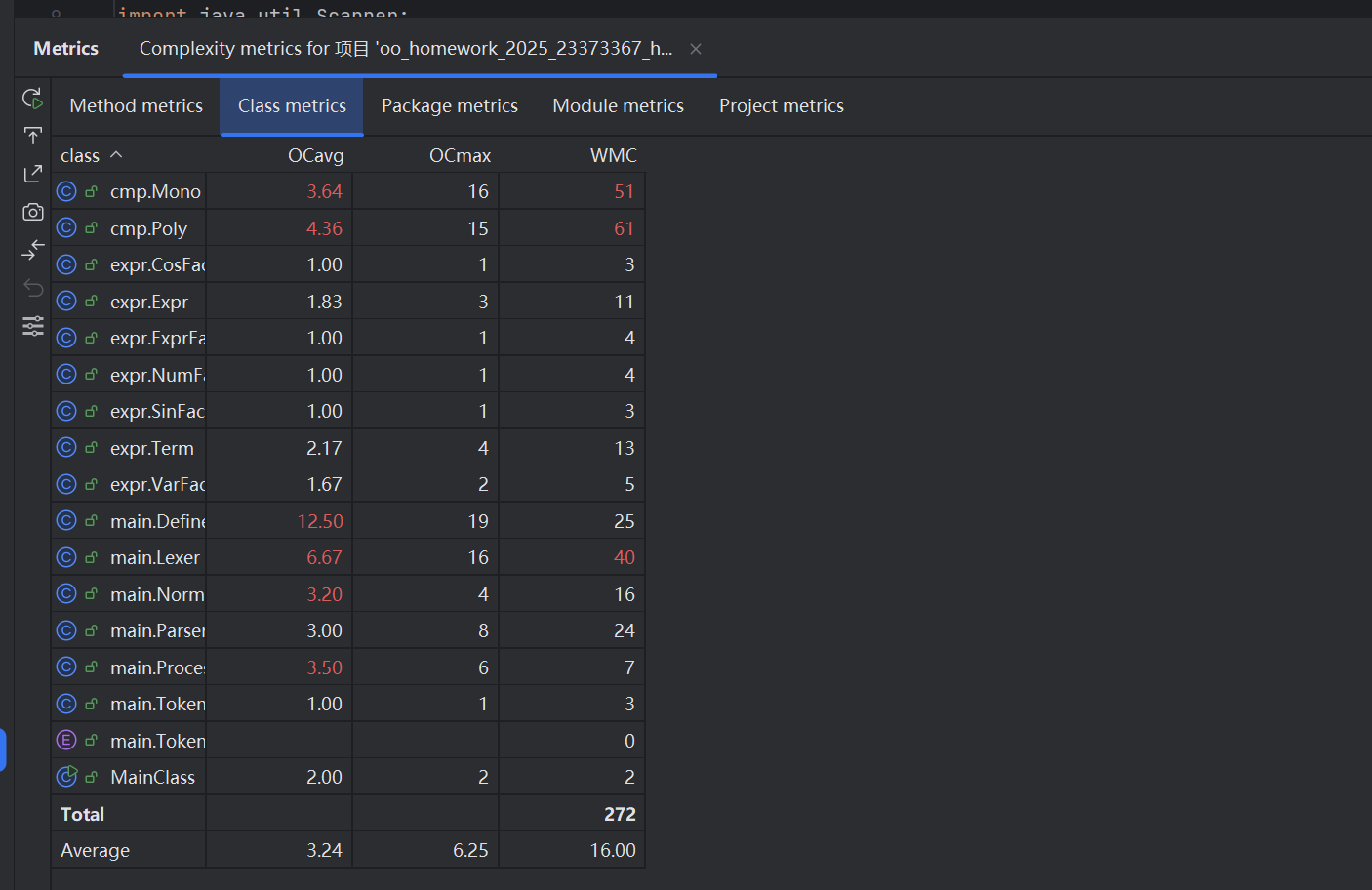
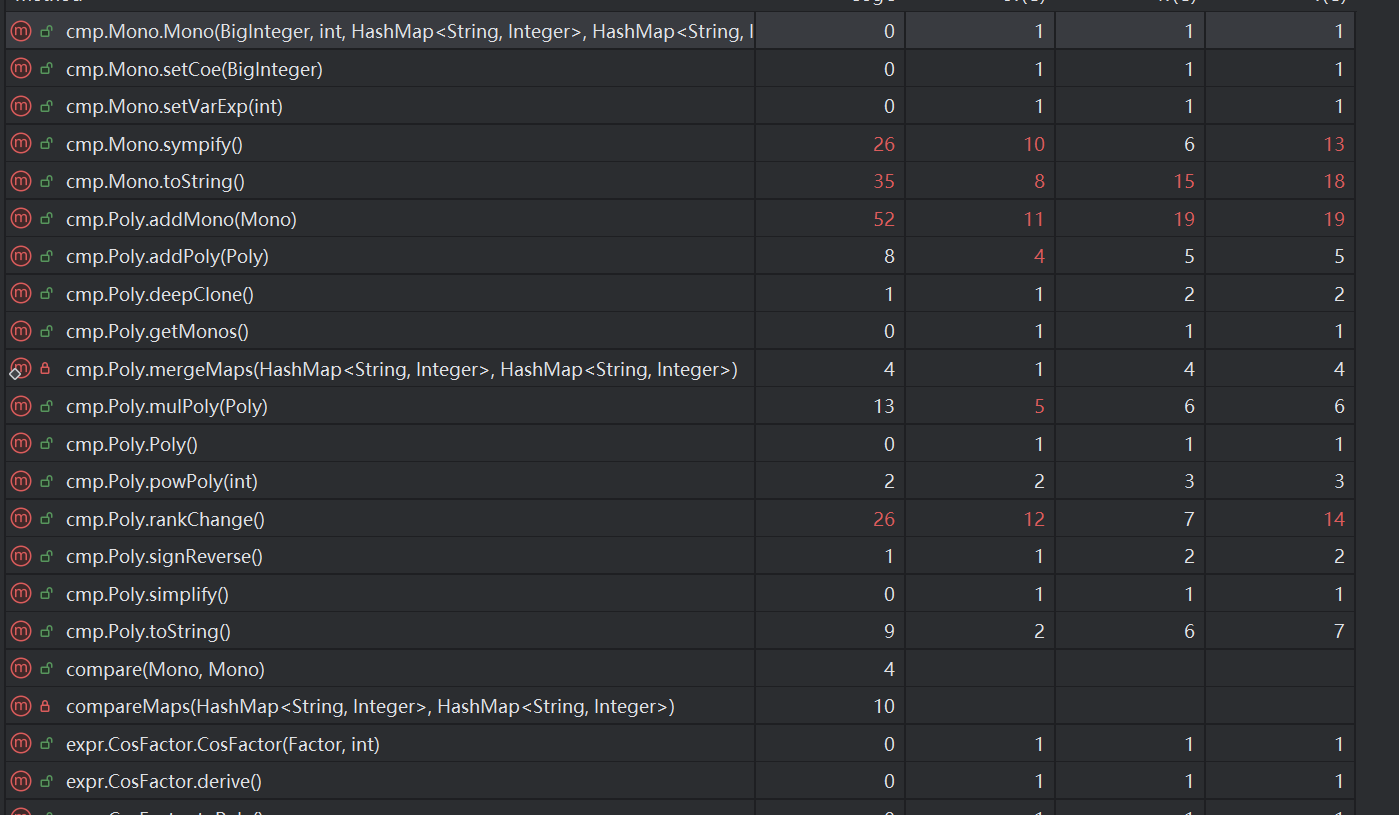
Method_Metrics_1

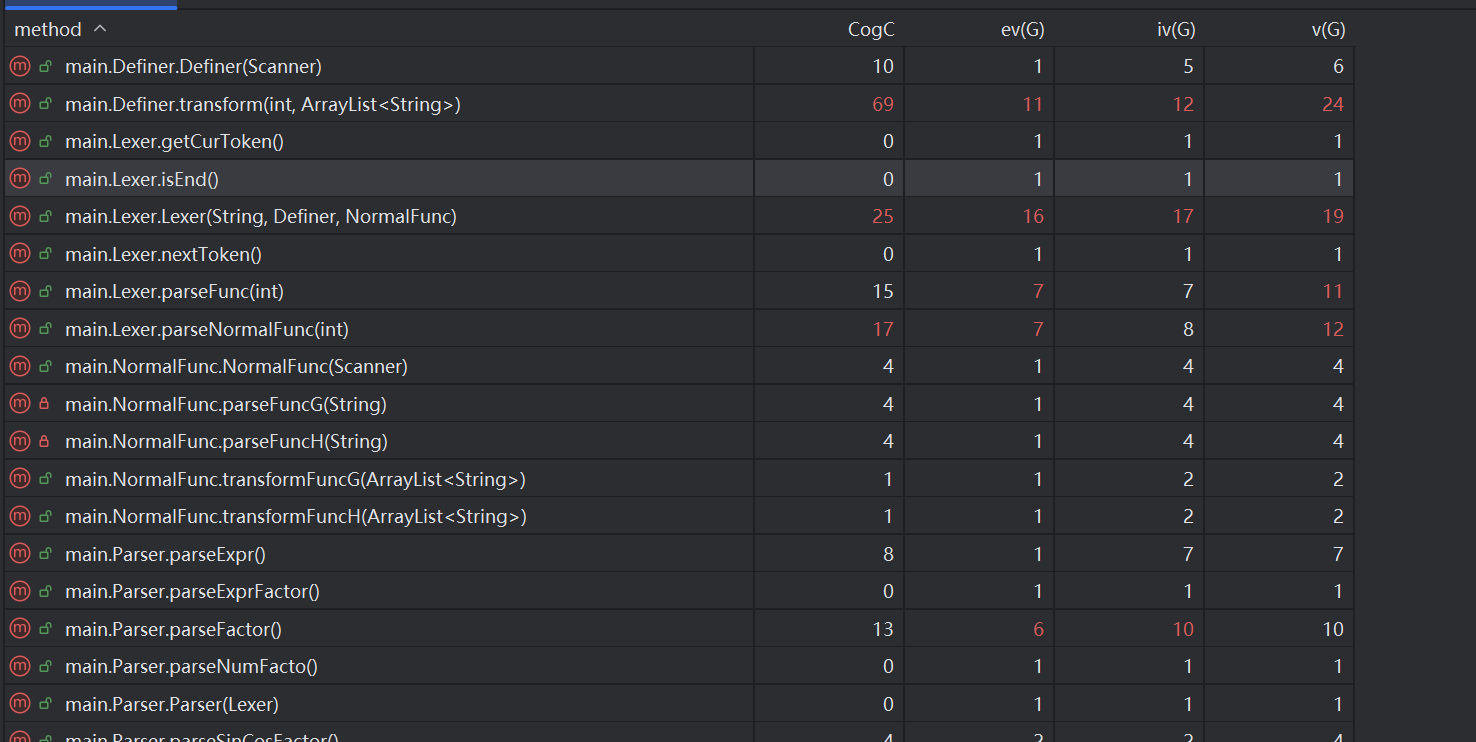
Method_Metrics_2

摘取复杂度较高的加以分析：

  • cmp.Mono.toSTring():该方法是重写了Mono的toString方法，在其中实现了对于系数为正负一和0，指数为0和1，sin和cos中的因子为1的特殊情况的输出，分支结构较多，使得其复杂度较高
  • cmp.Mono.sympify()&&cmp.Poly.addMono():在两分法中分别实现了二倍角和sin^2+cos^2=1等的三角函数的化简，在其中有较多的循环遍历结构与分支判断和跳转等
  • main.Definer.transform()：该方法进行了自定义递归函数的解析，是一个递归调用结构，有复杂的实参和形参识别与转换的问题，方法的复杂度较高
  • …

类间的耦合分析

Mono与Poly类中的复杂度指标均比较高，其承担了主要的计算功能，与所有的存储类均有关系。所有的存储类对象均转换为计算类对象加以分析计算，相互之间耦合度较高

Lexer中的复杂度也较高，其在遍历划分最小处理单元阶段就调用Definer.transform()方法进行化简，可能使得代码架构不清楚，反而增加了两个类的耦合度。完全可以将递归函数调用因子的解析交由Parser完成，这也与Lexer和Parser的类的功能定位相同

心得体会

本单元的学习并不轻松但也没有过于搞人心态。在第一次作业开始搭建前，我参考了作业训练，OOPre以及众多学长学姐的博客，进行了不错的代码架构，使得我并没有在之后作业中进行重构，整个单元的工作量并不是很大。

第二次作业迭代难度较大，既要进行架构调整还要进行三角函数优化。用我半成品的评测机课下测出了较多的bug并修改后，当我以为万事大吉的时候，又倒在了输出格式的问题上。第三次作业较为简单，在一个晚上速通之后自信心爆喷，没有进行充分的测试，直接喜提第一单元最低分。我认为OO作业的工作量可能不止来源于码字，还有测试。对于我这个评测机小白来说，写出来测试点生成逻辑已经耗尽所有心力。希望下个单元能和同学一起开发出一个合适的测评机，让我在强测和互测中不要过分狼狈。

感谢OO课上实验的不杀之恩（虽然并不完全确定课上实验做的是否完全正确，但起码没有CO实验带给我的巨大心理压力）

未来方向

总的来说，第一单元难度并不是很大，开学初大家课余时间也相对充裕。希望课程组可以在这段时间可以多出一些评测机搭建教程，方便评测机小白学习。

你可以在https://github.com/KingCB0501/BUAA_2025_OO的仓库中获得对应源码，与评测机（部分作业）。